Fourier Transform

Erasure Coding is a fundamental part of many algorithms and have a variety of use cases like securing data availability in blockchains and STARKs. And one of the key building blocks of Erasure Coding is Fast Fourier Transforms. Life is a full circle, right? I ran away from the course teaching Fourier Transforms as far as possible and here I am, trying to learn it again. But this time it’s different as curiosity has appeared wildly.

But you’re a dirty little liar with a message of obsession to come

You got your head in the clouds

And your world’s upside down

Get away from the life you’re living

Song time baby!! This time it’s Dirty Little Thing by Velvet Revolver. Oooooh, it’s a wild song. I couldn’t get the tune out of my head when I first listened to it.

DFT

Process to convert sequence of complex numbers $\{x_n\}:=x_0,x_1,\dots ,x_{n-1}$ to another sequence of complex numbers $\{X_n\}:=X_0,X_1,\dots ,X_{n-1}$.¹

$$\begin{array}{rl}\mathcal{F}& :C^N\to C^N\\ X_k& =\sum _{n=0}^{N-1}{x}_k{e}^{\frac{-2\pi i}{N}kn}\end{array}$$

IDFT

Interpolation

Vandermode

Vandermode matrix: $O(n^3)$

$$\left(\begin{array}{ccccc}1& x_0& x_0^2& \dots & x_0^{n-1}\\ 1& x_1& x_1^2& \dots & x_1^{n-1}\\ ⋮& ⋮& ⋮& \dots & ⋮\\ 1& x_{n-1}& x_{n-1}^2& \dots & x_{n-1}^{n-1}\end{array}\right)\left(\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_{n-1}\end{array}\right)=\left(\begin{array}{c}{y}_0\\ y_1\\ ⋮\\ y_{n-1}\end{array}\right)$$

Working With Polynomials

Tldr

• DFT: Coefficient representation → point-value
• Inverse DFT: Point-value → coefficient

An $n$-degree polynomial is represented in coefficient form:

$$A(x)=\sum _{j=0}^{n-1}{a}_j{x}^j$$

Lagrange coefficients:

$$A(x)=\sum _{k=0}^{n-1}{y}_k\frac{{\prod }_{j\ne k}(x-x_j)}{{\prod }_{j\ne k}{x}_k-x_j}$$

Algorithms and Time Complexity:

1. Addition/Subtraction: $O(n)$ in coefficient and point-value
2. Multiplication: $O(n^2)$ in coefficient and $O(n)$ in point-value and converting between the two can be done in $O(n\log n)$

Let the polynomial $A$ be defined with coefficients $a=a_0,a_1,\dots ,a_{n-1}$, with results $y_k$ for $k=0,1,\dots ,n-1$.

$$\begin{array}{rl}{y}_k& =A({\omega }_n^k)\\ & =\sum _{j=0}^{n-1}{a}_j{\omega }_n^{kj}\end{array}$$

Above equation is the DFT equation, represented as $DF{T}_n(a)$.

FFT

Lemma’s that help in understanding FFT:

1. Cancellation Lemma: ${\omega }_{dn}^{dk}={\omega }_n^k$
2. Halving Lemma: squares of nth complex root of unity are n/2 complex n/2th root of unity. $({\omega }_n^{k+n/2}{)}^2=({\omega }_n^k{)}^2$
3. Summation Lemma: ${\sum }_{j=0}^{n-1}({\omega }_n^k{)}^j=0$

Uses the following relation: $A(x)=A_{even}(x^2)+x{A}_{odd}(x^2)$.

$$\begin{array}{r}{y}_{even,k}=A_{even}({\omega }_n^{2k})\\ y_{odd,k}=A_{odd}({\omega }_n^{2k})\end{array}$$

Domain should be power of 2, and complex roots of unity, ${\omega }_n^i$.

Why does it need to be power of 2?

It actually depends upon the algorithm used, the most optimised Cooley-Tukey algorithm runs in $O(nlogn)$ time, and uses roots of unity as the domain. And Cooley-Tuckey uses $\omega$ properties to divide into length $k$, mostly 2. This is the radix property of the algorithm, thus it requires domain to order of length $k^r$.

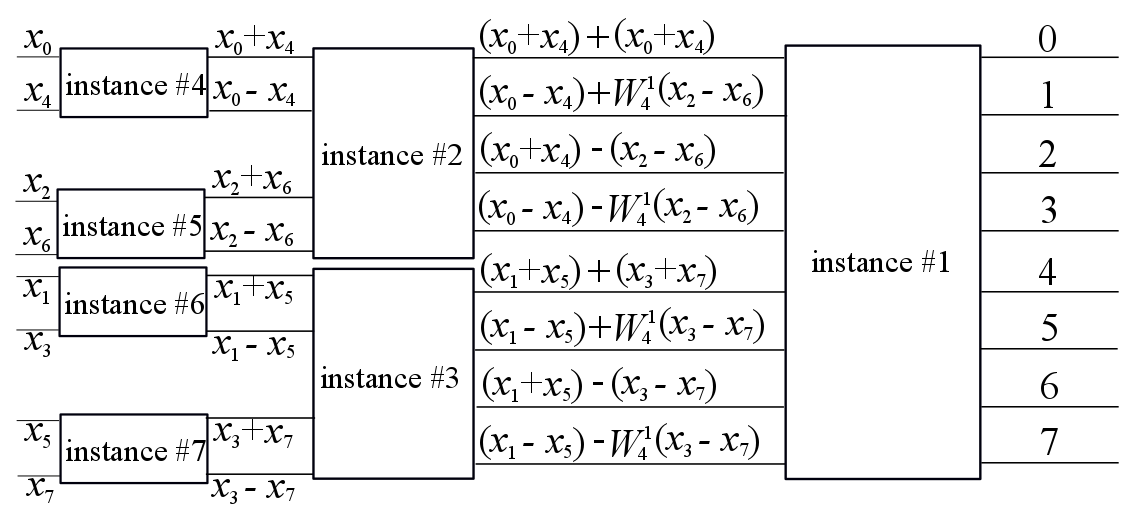
Let’s understand radix-2 Cooley-Tukey FFT algorithm

Cooley-Tukey Algorithm

Resources

• CLRS, Introduction to Algorithms, Chapter 30
• Radix-4 FFT
• FFT
• CP algorithms: FFT
• FFT over Finite Fields
• Ingonyama’s NTT 201
• Cryptography Caffe’s NTT: Part 1 & Part 2

Footnotes

1. Discrete Fourier Transform ↩