Verkle Trees is one of the big change that is going to be included in the Ethereum protocol towards its push to weak statelessness. There are much better resources to understand the reasoning behind going for statelessness.
In a Verkle trie, inner nodes are -ary vector commitments to their children instead of hashes like a merkle trie. The root of a leaf is hash of the (key, value) pair, and root of an inner node is hash of the vector commitment. So, naively to prove value of a leaf, you only require values.
- tree of some depth
- to prove leaf node
- need proofs/hashes to prove a leaf in case of merkle trees
- But for verkle tries, proofs are in terms of vector commitments i.e. . Polynomial commitments most efficient and simple vector commitments
- thus require, commitments and proofs
- each commitments would me in terms of a polynomial, where commitment
- domain in terms of , i.e. th root of unity.
But fortunately in case of polynomial commitments, instead of giving commitment and proof for each level, we can combine the proof and give a multiproof that convinces the verifier that value of a leaf node is indeed what we want to prove. Following is the steps of a scheme that generate multiproof using random evaluation.
Proof
Given commitments , prove evaluations where and is a -th root of unity.
-
Generate
-
Prover encode all proofs in a polynomial
Now, we just have to prove that is indeed a valid polynomial (not a rational function). This can be done by committing to this polynomial , evaluating it at a random point and verifier verifying it.
-
Prover create a commitment
-
evaluate at point , where
-
can be computed by verifier as all the inputs are known
-
⇒ can also be computed by verifier
-
Prover gives the proof
-
Verifier verifies via
This allows us to prove an arbitrary number of evaluations.
- Proof is also constant size (one commitment , one number , two proofs).
- , values do not need to be explicitly provided
- Only leaves keys and values, and corresponding commitment to each level are required
- For and , the average depth comes out to be .
Design Goals
- Cheaper access to neighbouring code chunks and storage slots to prevent thrashing
- distribute data as evenly as possible in the tree
- Fast in SNARKs
- Forward compatible, i.e. interface should be pure (key, value) pair of 32 bytes.
Reasoning for Pedersen Commitments
Now, there are two commitment schemes that can be used for vector commitments.
- KZG Polynomial commitments
- Pedersen Vector commitments + IPA (Inner Product Arguments)
Ethereum has decided to go with Pedersen commitments citing following advantages:
- No trusted setup
- Everything can be done inside a SNARK as well
- Developed new curve (Bandersnatch) that “fits inside” BLS12_381 (outer field = curve order)
- Future proof for witness compression and zk-rollups
Disadvantage: Not as efficient for proving a single witness. But this is not very important to us.
Changes in Tree Structure
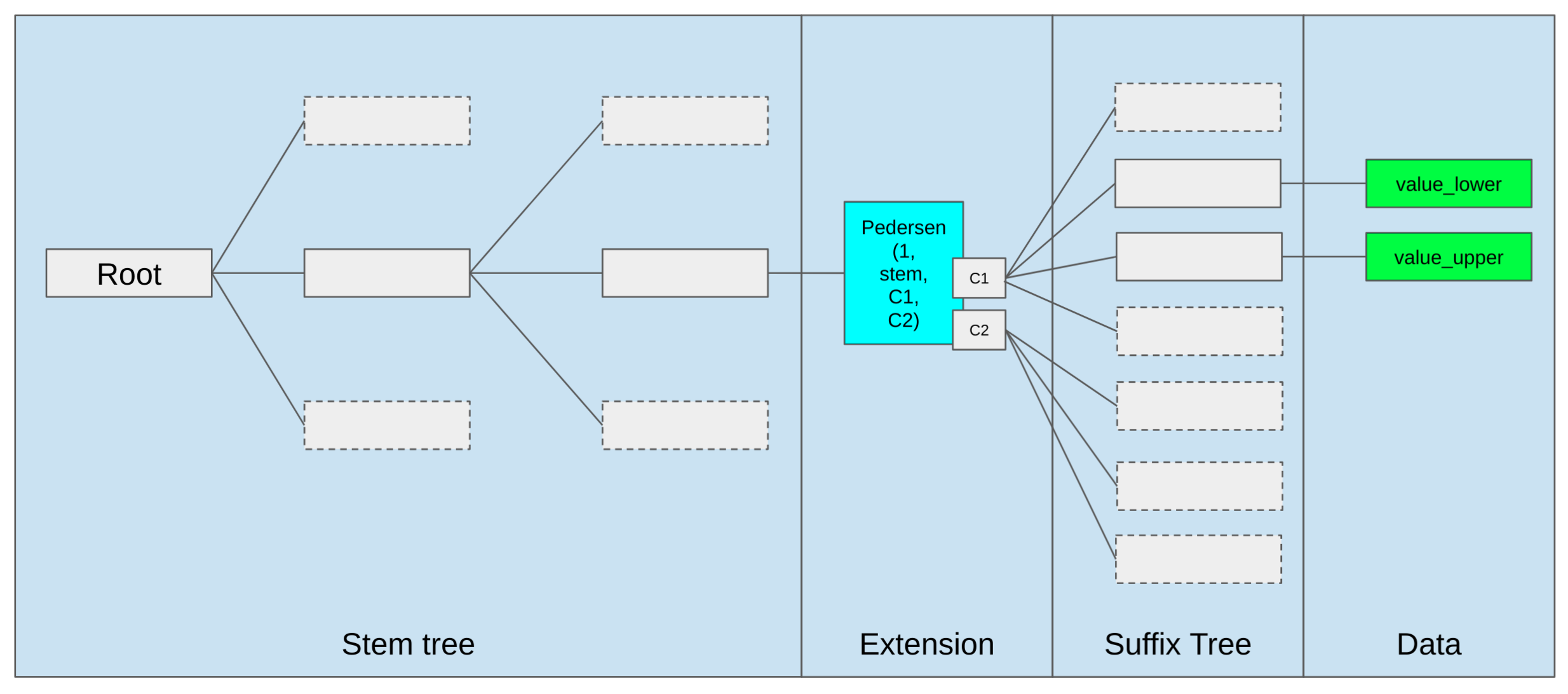
Verkle Trees introduces a number of changes in the tree structure.
- Shifting from 20 bytes keys to 32 bytes
- tree width from hexary to 256
- vector commitments instead of hashes
- merge of account and storage tries
- gas changes
ETH Verkle Explainer