Once again, this is just another of my notes aggregated from various sources. This is a very dumbed down version for just my understanding and it’s my advice to follow the resources attached as they are more thorough and detailed explained by experts on the topic. I’m just a novice who is interested in learning cryptography.
Walking side by side with death
The devil mocks their every step
The snow drives back the foot that’s slow
The dogs of doom are howling more
Now, for the song. This time we’ll listen No Quarter by Led Zeppelin. No description for this. I guess they don’t need one :)
Discrete Logarithm Problem
Discrete logarithm Problem (DLP) for a group and an element is,
Given an element in the subgroup generated by , find an integer satisfying .
This can be computed using . DLP for some groups is said to be very easy and for some difficult which allowed cryptographers to experiment with it and invent some amazing primitives in cryptography.
DLP is easy for:
- under addition
- or under multiplication
And for some groups, it is difficult but not computably infeasible:
- under multiplication: said to be sub-exponential
Elliptic Curves

This is a curve defined in plane .
- Above equation is called the general Weierstrass equation. is the point at infinity.
- is the algebraic closure of field .
- Can be defined on any fields, such as .
- EC defined on are finite groups.
- ECDLP is discrete logarithm problem for the EC defined on finite field which has exponential time complexity to solve.
- Best known algorithm for an EC defined over takes .
We make simplification of the general equation with the case when field characteristic is not 2 or 3. Define curve read as curve over field . This gives rise to short Weierstrass equation form of the EC.
Coordinate System
Affine Coordinates
Traditional representation of the coordinates, i.e. just an where and satisfy curve equation. Normally this representation is used for storing and transmitting points.
Standard Projective Coordinates
Point in standard projective coordinates represents in Affine coordinate system. Also called homogeneous projective coordinates as the curve equation takes on the homogeneous form .
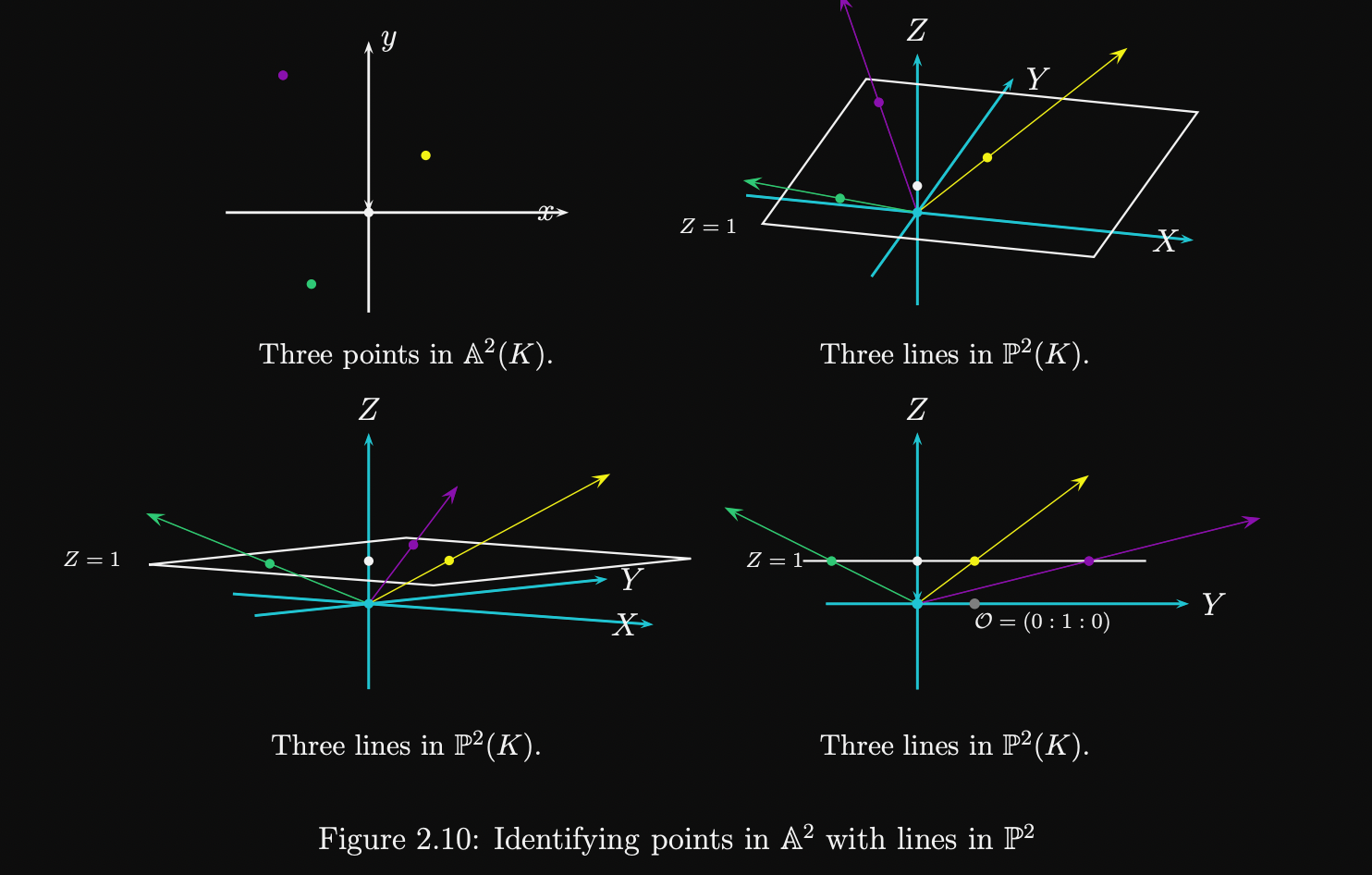
Points become straight line through the origin in space, with the affine point being the intersection of the line with the plane . Equivalence relation from plane to projective space can be defined as:
Jacobian Coordinates
Jacobian Point → . Curve equation becomes .
Group Law of Elliptic Curves
- Elements of the group are points on elliptic curve.
- identity element is the point at infinity
- inverse of point is symmetric about -axis
- addition rule: given three aligned, non-zero points on EC,
Elliptic Curves in
Every EC has an order which represents the number of points on the curve. This can be explained using group theory. Let’s say we have a group, and the order of group denotes the number of points on the group. Now, if we take a point on the curve, then it tends to repeat itself in a cycle after some points. An amazing animated tutorial for elliptic curve in can be found here.
For Example: Let’s take a curve and the point . The multiples of P are just 5 distinct point on the curve and they are just repeating themselves.
This makes set of the multiples of a cyclic subgroup of the group formed by the elliptic curve. The point is called the generator or base point of the cyclic subgroup. Finding order of the subgroup is done by finding smallest such that .
Normally, curves are defined for large prime fields, where short equation covers all possible isomorphism classes of elliptic curves. 1
There are other ways to express an elliptic curve:
- Montgomery equation , where in . substituting and gives short weierstrass equation.
- Edwards equation , substituting and produces montgomery equation.
What is the difference between these curve equations? And how does one is beneficial over other?
Concisely answered here and here. Expanding on this, montgomery ladder is faster than standard Weierstrass point multiplication methods as montgomery ladder is constant-time. There is very concise explanation about Curve25519 by Martin Klepmann.
Montgomery curve
Why montgomery form is better for multiplication?
Edwards curve
TODO
Twisted Edwards curve
There is a 1:1 correspondence between TEd curves and Mont curves. In a more cryptographic glossary, every Twisted Edwards curve is birationally equivalent to Montgomery curve2. To convert a curve from Twisted Edwards form to montgomery form:
We can also convert a montgomery curve to Twisted Edwards curves using following equation:
Resources
- ethereumbook’s elliptic curve section
- An Introduction to Elliptic Curves
- Exploring Elliptic Curve Pairings
- BLS12-381 for the rest of us
- Pairings over BLS12-381
- EC domain parameters
- choosing safe curves for elliptic-curve cryptography
- The animated elliptic curves
- Elliptic Curve Cryptography: a gentle introduction
- An introduction to elliptic curves
Footnotes
-
Pairings For Beginners Page 14 ↩
-
Birationally equivalent just means that a map exists between two objects and is invertible. ↩