IOP defines as interactive oracle proofs are denoted by a system of interactive randomised algorithms where interaction happens between entities involved in the system: . Verifier is given oracle access to the message sent by prover to the verifier in any round.
Properties of an IOP system:
- Round complexity, : number of rounds of interaction between and
- Proof length, : sum of length of all messages sent by
- Proof complexity, : number of entries read by from the various prover messages
PIOP
Polynomial interactive oracle proofs are interactive protocols between prover and verifier where with each message, prover creates an oracle and verifier can query any oracle supplied by the prover.
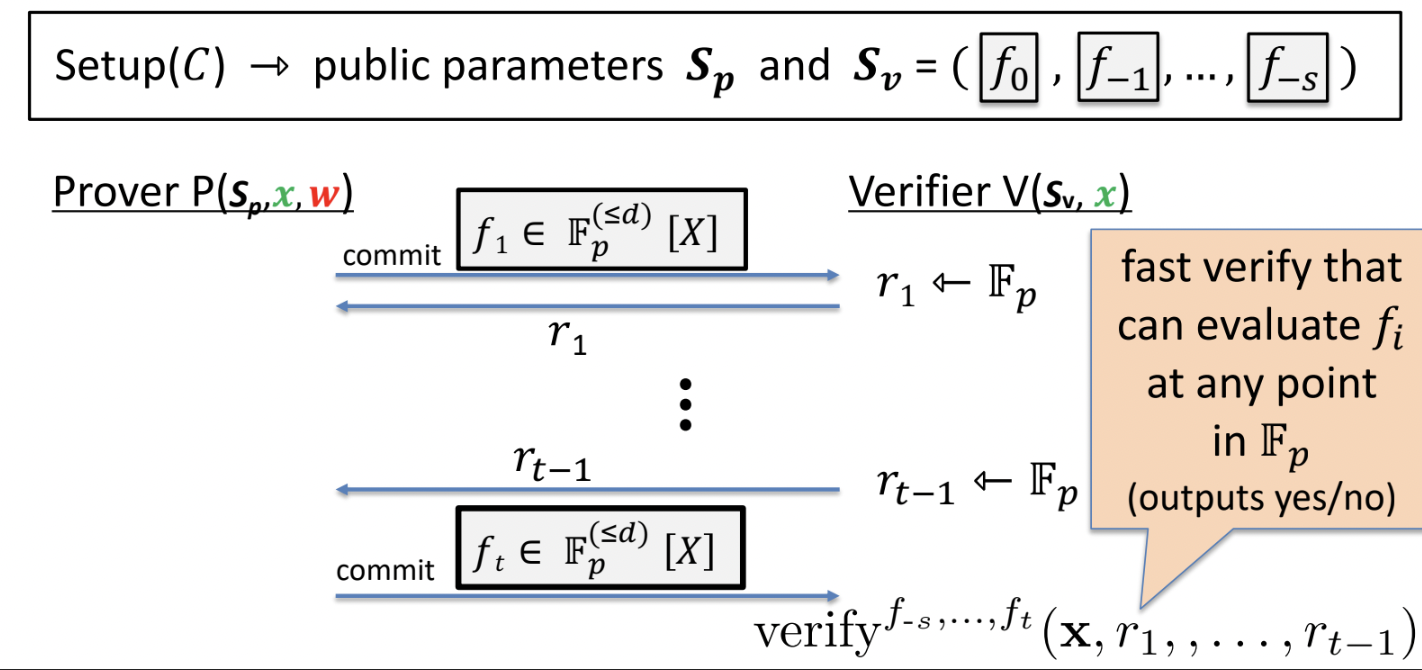
Method to convince verifier that the proof generated by prover is correct.
:- setup procedure of circuit
:- consists of commitments to polys.
- Why does contains commitments to different polynomial?::maybe due to having different sets of polynomial for each part of circuit.
- What if prover commits to a zero polynomial? i.e. what if :: then we can do zero test on polynomial. i.e. take a random point in and test whether it’s zero or not. and prob. of being zero is negligible with value where d is the degree of polynomial. example:
- what if prover commits to same polynomial? :: do equality test, take if , then with very high prob. Not straightaway understandable to me tho.
- Prover sends t commitments to verifier
- verifier sends t random values to prover
- verifier runs a verify algorithm taking all the commitments and the random values, and previously generated setup summary , i.e. commitments to polynomials.
- It can ask prover to open any of the commitment at any point.
- Verifier accepts/reject the proof.
Poly-IOP:
- : no. of commitments to polynomials
- : no. of eval queries in verify
- Prover sends commitments
- Verifier verifies at evaluations by running PCS eval.
Info
Length of SNARK: commitments + eval proofs
Verifier time:
Prover time: