SNARKs

Properties that any zero knowledge based proving system needs to entertain:

1. Completeness: Any honest prover can convince verifier of the statement and witness.
2. Soundness: Any malicious prover can never convince a verifier of the statement that it’s trying to prove. In other words, if a prover doesn’t know witness, it can never convince the verifier.

Any proving system defines an n-variate polynomial with an evaluation recipe. Two parties involved in the process are Prover and Verifier.

What is the difference between proof and argument of knowledge?

SNARKS are succinct argument of knowledge: Mostly used interchangeably but in proofs the soundness holds against a computationally unbounded adversary while in argument of knowledge soundness only holds against polynomially unbounded adversary. Arguments are thus called computationally sound proofs.

SNARK

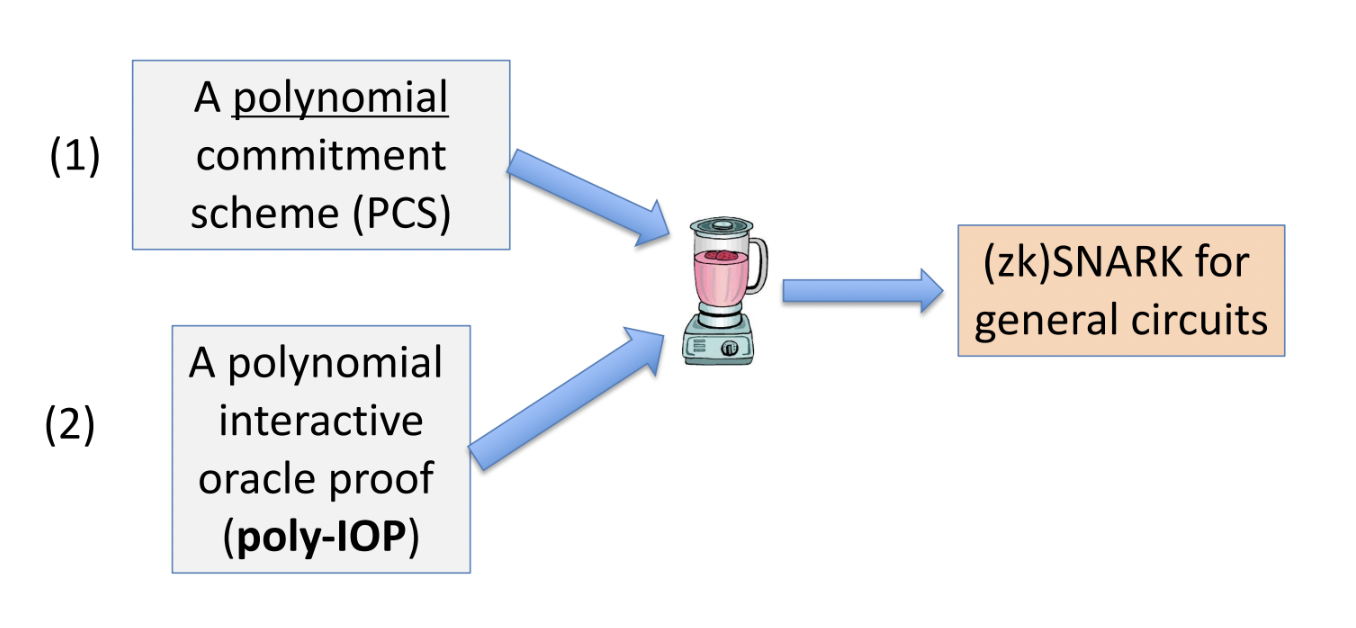
Argument system that generate succinct and fast proofs for public statement $x$ in ${\mathbb{F}}^n$ and secret witness $w$ in ${\mathbb{F}}^m$. The statement and witness need to be encoded in an arithmetic circuit $C$.

Arithmetic circuits: $C(x,w)\to \mathbb{F}$

Requirements:

1. Completeness: $\forall x,w:C(x,w)=0\to Pr[V(S_v,x,P(S_p,x,w))]=1$
2. Knowledge Sound: P doesn’t know $w\to Pr[V(S_v,x,\pi )]=$ negligible

why are finite fields important for SNARKs?

Because of hard DLP, group operations, roots of unity.

More formal definition:

Soundness

For dummies like me: for every polynomial time adversary, there exists an extractor that uses adversary to find out about $w$, even though adversary doesn't know about $w$, because if it would, then adversary can generate arbitrary proofs.

(S,P,V) is knowledge sound for a circuit if for every poly. time adversary A = (A_0, A_1) such that:

$$\begin{array}{rl}S(C)& \to (S_p,S_v)\\ (x,state)& \leftarrow A_0(S_p)\\ w& \leftarrow A_1(x,S_p,state)\end{array}$$

there is an efficient extractor $E$, that uses $A_1$ s.t.

$$\begin{array}{rl}S(C)& \to (S_p,S_v)\\ (x,state)& \leftarrow A_0(S_p)\\ w& \leftarrow E^{A_1(x,S_p,state)}(S_p,x)\end{array}$$

Zero Knowledge

For any normal proof, there exists a simulator which can generate proofs without knowledge of $w$.

(S,P,V) is zero knowledge for circuit C if there is an efficient Sim s.t. $\forall x\in {\mathbb{F}}^n\to \exists w:C(x,w)=0$, the distribution:

$(C,S_p,S_v,x,\pi ):\text{where}(S_p,S_v):S(C),\pi :P(S_p,x,w)$

is indistinguishable from the distribution:

$(C,S_p,S_v,x,\pi ):\text{where}(S_p,S_v,\pi )\leftarrow Sim(C,x)$

Proofs

Two ways to prove statement:

• Interactive: prover and verifier goes back and forth to agree on some random values and parameters which verifier can then verify.
• Non-interactive: Pre-processing done to generate a proof $\pi$ that allows verifier to verify circuit.

Preprocess argument system: prover preprocesses $C$ to generate public parameters $S_p,S_v$.

Consists of $(S,P,V)$:

• $S(C)$: generate $S_p,S_v$
• $P(S_p,x,w)$: generate proof $\pi$
• $V(S_v,x,\pi )$: verify proof

How does $S_p,S_v$ gets generated? Is it done for every circuit or some other method? Wouldn't it be very bad UX if we have to run $S$ every time?: Each circuit needs some summary that can be used to verify the proof as no verifier will run the whole computation again, otherwise there's no benefits of these systems.

There has to be some randomisation involved that prover can’t forge by itself to generate these parameters.

• First method is to generate random $r$ for every circuit outside prover.
• Second is to generate a random value once $S_{init}(\lambda ,r)\to pp$, create some public parameters based on that, use those parameters to generate $S_{index}(pp,C)\to S_p,S_v$
• Totally transparent: no random secrets needed to generate circuit parameters.

---

Pipeline followed by any ZKP system:

flowchart LR
A["computation"]
B["circuit"]
C["prover"]
D["IOP"]
E["verifier"]
A-- arithmetisation --> B
B-->C
C-->D
D-->E

Any circuit need to be proven to verifier, so we need to encode and evaluate our polynomial. Thus, most SNARK system consist of two components:

1. Functional commitment scheme (FCS)
2. Interactive oracle proofs (IOP)

PLONK: poly-IOP for General Circuit

Plonk IOP can be used with different PCS to generate different proving systems. For example:

1. Aztec’s proving system: KZG+Plonk
2. Halo2: Bulletproofs + Plonk, used by zcash
3. Plonky2: FRI + Plonk, used by polygon zkevm
4. Scroll: (halo2) plonk + kzg

Step 1: Compile Circuit for a Computation Trace

Suppose you have a circuit with inputs $I:I_x,I_w$, and gates C where $x$ is the statement inputs and $w$ is the witness input. Our goal is to prove to verifier that $C(w)=0$.

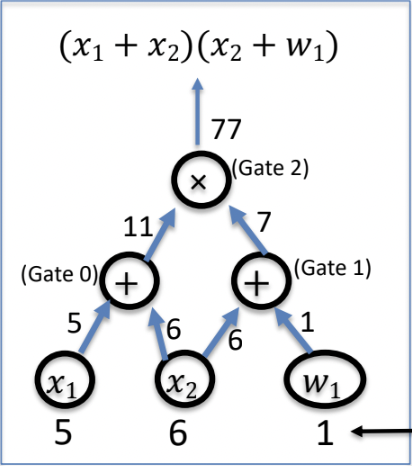
We put inputs $x_1=5,x_2=6,w_1=1$, and compute the computation trace through the circuit. The computation trace comes out to be:

inputs:	5	6	1
Gate 0:	5	6	11
Gate 1:	6	1	7
Gate 2:	11	7	77 ← Output

Step 2: Encode Trace in Polynomial $P$

• Calculate $d$ of $P$ = $3|C|+|I|$ where |C|: no. of gates and |I|: no. of inputs
• Aim: encode in a polynomial of form: $F_p^{(<=d)}(X)$
• Encode inputs: $P(w^{-i})=I_i\forall i\in I$
• Encode gate $l\in C$ wirings:
  • $P(w^{3l})=$ left input to gate l
  • $P(w^{3l+1})=$ right input to gate l
  • $P(w^{3l+2})=$ output of gate l
• Prover has $d$ evaluations of $P$, can use FFT to interpolate coefficients in $O(lo{g}_{2}d)$

Step 3: Prove Validity of P

What does prover needs to prove to verifier in order to convince it?

• correct output: to prove that output of computation was according to the statements and witness committed.
• correct inputs: proves
• correct intermediate gate evaluations:
• wiring between gates is according to the statement specified by prover

Proof Gadgets for IOP

• equality test → to test if polynomial $f$ and $g$ are equal and note that verifier only has the commitment, verifier queries the polynomial at point $r$ or opens the commitment and test if values providied by prover are equal. But this generates soundness error.
• soundness error → two polynomials in ${\mathbb{F}}_p$ can be zero at at most d roots, if $f(r)-g(r)=0=>f-g=0=>f=g\text{v.h.p}$
  • this assumption has error d/p such that if suppose g is not same as f, then g can have at most d different roots. thus, error → $d/p$
  • this is derived from Schwartz-Zippel Lemma

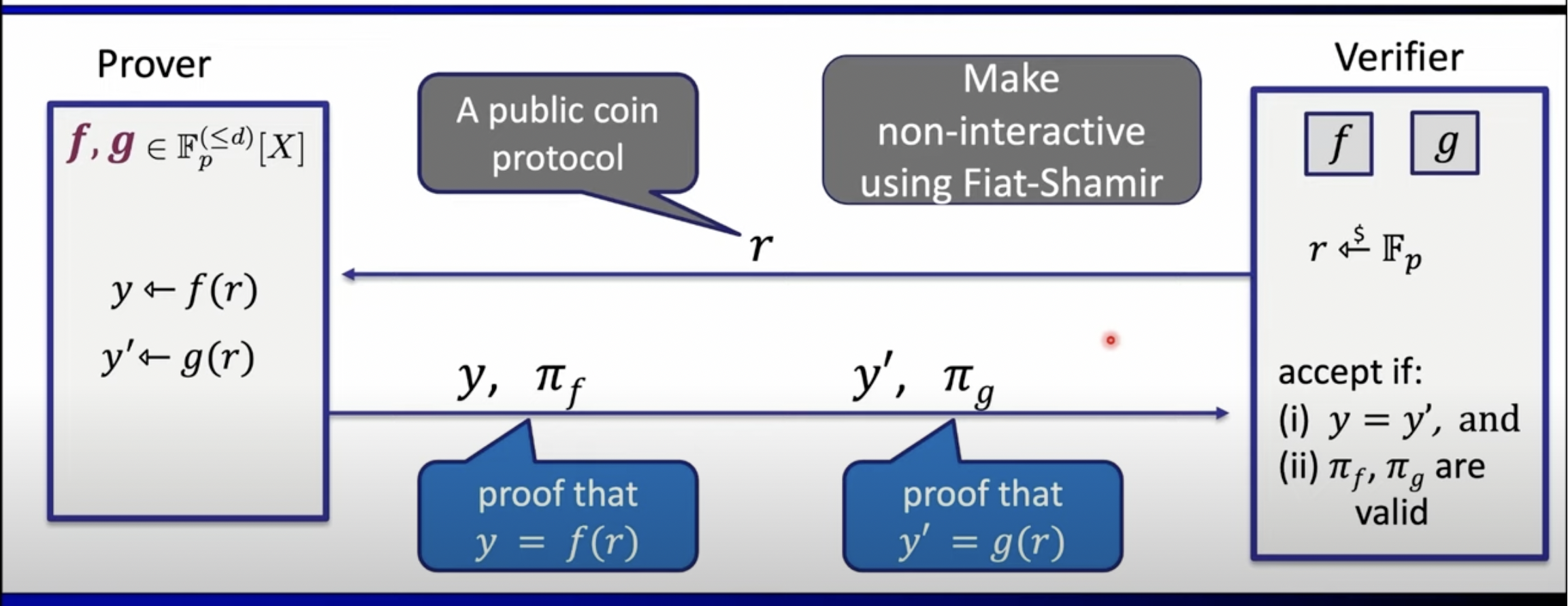
let $\text{Upomega}$ be some subset of ${\mathbb{F}}_p$ of size $k$. Let $f\in {\mathbb{F}}_p^{<=d}[X]$ be the polynomial that prover wants to prove. Verifier has commitment to this polynomial $Com(f)$.

We can construct efficient poly-IOPs for the following tasks:

1. Zero Test: Prove that $f$ is identically zero on $\text{Upomega}$
2. Sumcheck: Prove that ${\sum }_{a\in \text{Upomega}}f(a)=0$
3. Product check: Prove that ${\prod }_{a\in \text{Upomega}}f(a)=1$
4. Permutation check: Prove that $f(a)=g(W(a))$ where $W$ is a permutation polynomial.

Question

• Why do we do these checks only? What is the significance of these checks? What other checks can be done? Can we remove some checks or combine some checks?
• How does the permutation polynomial is calculated?
• Find the reasons behind these checks? Could you have come up with these yourselves?

Vanishing Polynomial of $\text{Upomega}$ is $Z_{\text{Upomega}}(X):={\prod }_{a\in \text{Upomega}}(X-a)$. $Deg(Z_{\text{Upomega}})=k$ If $\text{Upomega}$ becomes the multiplicative subgroup formed using primitive $k^{th}$ root of unity, then VP becomes $X^k-1$. Thus, VP can be calculated in logarithmic time.

Zero Check

Let $\text{Upomega}=1,\omega ,\cdots ,{\omega }^{k-1}$. Calculate $q(X)=f(X)/X^k-1$.

Send $Co{m}_q$ to verifier, and verifier opens commitment at point $r$, and check $f(r)=q(r)(r^k-1)$. This proves that f(x) is divisible by X^k-1, hence, f has roots in $\text{Upomega}$.

Sum Check

Read Sumcheck

Product Check on $\text{Upomega}$

We want to prove ${\prod }_{a\in \text{Upomega}}f(a)=1$. Naively, we can send all evaluations of $f$ in $\text{Upomega}$ but that will be quadratic in degree d. Instead, we can create a polynomial $t\in {\mathbb{F}}_p^{<=k}(X)$ that evaluates to 1 at ${\omega }^k-1$.

Let’s try a toy example in sage taken from here:

// verifying that f(x)=c in GF(17) for w = 4
F17 = GF(17)
R17.<x> = PolynomialRing(F17)
w = F17(4)
c0 = F17(2)
c1 = F17(3)
c2 = F17(4)
c3 = F17(5)
c = c0*c1*c2*c3
points = [(w^0, c0), (w, c1), (w^2, c2), (w^3, c3)]
R17.lagrange_polynomial(points)

So, we can define polynomial $t$ s.t. $t(1)=1,t({\omega }^s)={\prod }_{i=0}^{s}f({\omega }^i)$ for s=1,…,k-1. Now in order to prove product check, we’ll prove:

1. $t({\omega }^{k-1})=1$
2. $t(\omega .x)=t(x).f(\omega .x)$ for all $x\in \text{Upomega}$. This will be used to a zero test on t(X) so that verifier can get convinced that prover actually computed $t(x)$. This is proven using: $t(\omega r)-t(\omega )f(\omega r)=q(r)(r^k-1)$.

The same product check holds for rational function as well, i.e. $f/g$. Prove this using: $t(\omega x)g(\omega x)=t(x)f(\omega x)$

Permutation Check

It is used to check that two polynomials $f,g$ are permutation of each other. Mainly, prover wants to prove that: $(f(1),f(\omega ),\cdots ,f({\omega }^{k-1}))\in {\mathbb{F}}_p^k$ is a permutation of $(g(1),g(\omega ),\cdots ,g({\omega }^{k-1}))\in {\mathbb{F}}_p^k$.

Can be done by creating two polynomials $\hat{F}={\prod }_{a\in \text{Upomega}}(X-f(a))$ and $\hat{G}={\prod }_{a\in \text{Upomega}}(X-g(a))$ and doing product check on these two polynomials. How will the product check work? It’s simply testing that $\frac{\hat{f}(r)}{\hat{g}(r)}={\prod }_{a\in \text{Upomega}}\left(\frac{r-f(a)}{r-g(a)}\right)=1$.

Why can't we do zero test to check that these polynomials are equal? ::

Prescribed Permutation Check

Instead of just proving the permutation, prover wants to prove that $f(x)=g(\sigma (x))$, where $\sigma :\text{Upomega}\to \text{Upomega}$ is a permutation if $\forall i\in [k]:W({\omega }^i)={\omega }^j$ is a bijection.

Why can't you use zero check here to check the two polynomials are equal? :: because g(W(y)) where y in $\text{Upomega}$ will become O(d^2) in prover time. We don't want quadratic time prover.

Observation: If $(\sigma (a),f(a){)}_{a\in \text{Upomega}}$ is a permutation of $(a,g(a))$ then $f(y)=g(\sigma (y))$. We prove this by defining bivariate polynomial:

$$\begin{array}{rl}\hat{f}(X,Y)& =\prod _{a\in \text{Upomega}}(X-Y.\sigma (a)-f(a))\\ \hat{g}(X,Y)& =\prod _{a\in \text{Upomega}}(X-Y.a-g(a))\end{array}$$

We do product check on these two polynomials such that ${\prod }_{a\in \text{Upomega}}\left(\frac{r-s.\sigma (a)-f(a)}{r-s.a-g(a)}\right)=1$, where $r,s$ is the input queried by verifier.

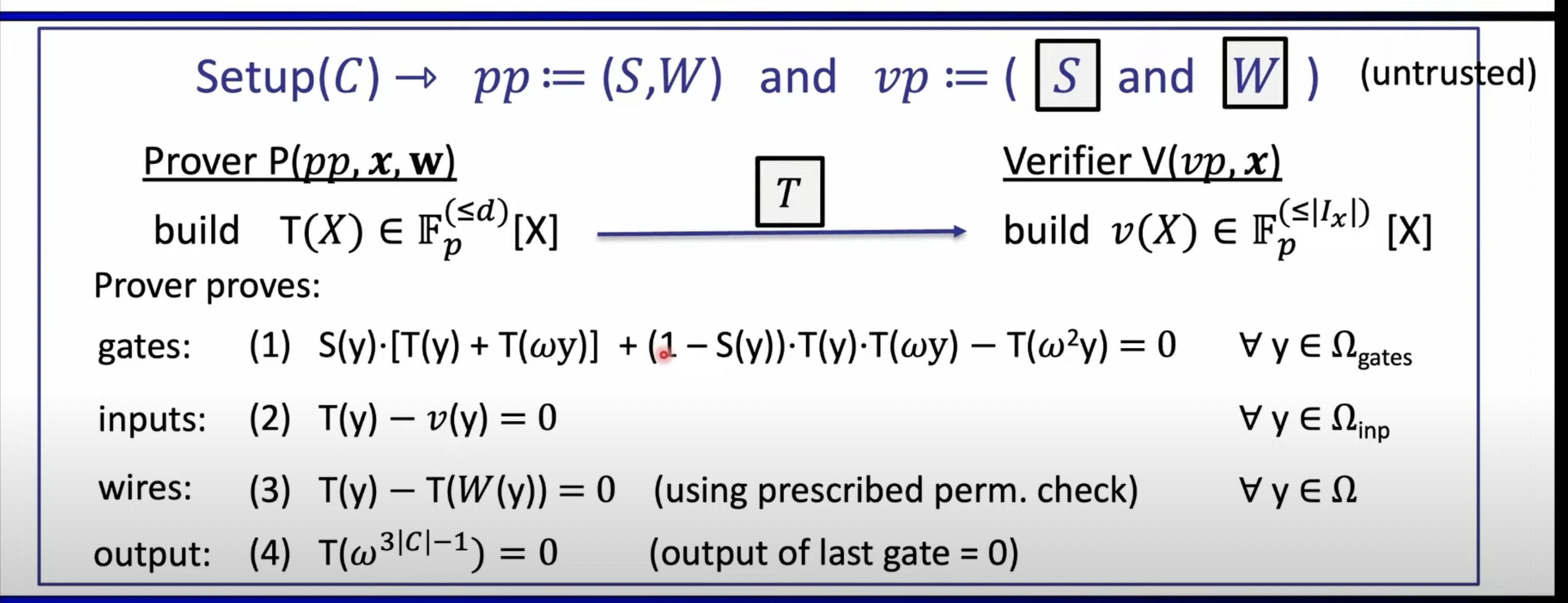
Proving Validity of T(x).

T(x) is the polynomial that encodes the computation trace of the circuit.

Prove Inputs Were Correct.

Create polynomial v(y) on ${\text{Upomega}}_{inp}:=\{{\omega }^{-1},{\omega }^{-2},\cdots ,{\omega }^{-|Ix|}\}\subseteq \text{Upomega}$ and do zero test on:

$$T(y)-v(y)=0\forall y\in {\text{Upomega}}_{inp}$$

Prove Gate Evaluations Are Correct

Define a selector polynomial S(X) which is:

1. $S({\omega }^{3l})=1$ if gatel is an addition gate.
2. $S({\omega }^{3l})=0$ if gatel is a multiplication gate.

Then, you define the polynomial:

$S(y)[T(y)+T(wy)]+(1-S(y))[T(y).T(wy)]=T(w^{2}y)$

then it’s just the zero check.

Combining Gate Constraints into One Equation

You can very easily combine gate constraints into one equation:

$$\begin{array}{c}{Q}_L(x)a(x)+Q_R(x)b(x)+Q_O(x)c(x)+Q_M(x)(a(x).b(x))+Q_C(x)=0\text{label}eqa\end{array}\text{\hspace{1em}(1)}$$

where,

1. $Q_L,Q_R$: selector polynomial created for evaluation for left, right of a gate respectively.
2. $Q_O$: selector polynomial for addition gate.
3. $Q_M$: selector polynomial for multiplication gate.
4. $Q_C$: polynomial for constant in a gate, ex: public inputs of the circuit.
5. $a(x),b(x),c(x)$: polynomial for left, input and output values of the gates.

We can rewrite $\text{eqref}eqa$ in terms of linear factors in ${\omega }^i$,

$$\begin{array}{c}{Q}_L(x)a(x)+Q_R(x)b(x)+Q_O(x)c(x)+Q_M(x)(a(x).b(x))+Q_C(x)=(x-\omega )\dots (x-{\omega }^n)h(X)\end{array}$$

Term $(x-\omega )\dots (x-{\omega }^n)$ is Vanishing Polynomial:$H(X)$. Since, $\omega$ is a primitive nth root of unity, ${\omega }^i$ forms a cyclic group, and $H(X)=X^n-1$ . Plonk says that, constraint system is satisfied, when the constraint equation is completely divided by Vanishing polynomial.

$$H(X)|Q_L(x)a(x)+Q_R(x)b(x)+Q_O(x)c(x)+Q_M(x)(a(x).b(x))+Q_C(x)$$

Prove Gate Wirings Are Correct.

encode the wires as permutation polynomial and prove through permutation check that wiring along the circuit is correct.

$T(y)=T(\sigma (y))\forall y\in \text{Upomega}$

But we have three different n-degree poly, namely $a(X),b(X),c(X)$, thus we join these three polys into one polynomial of degree-3n:

$$u=x_l||x_r||x_o=(x_l^1,\dots ,x_l^n,x_r^1,\dots ,x_r^n,x_o^1,\dots ,x_o^n)$$

and create a permutation $\sigma \in S_{3n}$ on $u$ which gives $v$. $\sigma$ is chosen such that subset of array $u$ forms cycles.

Recap

Formal Protocol

Prover’s Algorithm

Round 1:

Compute $a(x),b(x),c(x)$ and send commitments $[a{]}_1,[b{]}_1,[c{]}_1$ to verifier.

Round 2:

• Compute permutation challenge $\beta ,\gamma$.
• Compute permutation polynomial $z(x)$ and send commitment $[z{]}_1$ to verifier.

Round 3:

• Compute quotient polynomial $t(x)$ and send commitment $[t_{low}(x){]}_1,[t_{mid}(x){]}_1,[t_{hi}(x){]}_1$ to verifier.
• It uses quotient challenge: $\alpha$ to distinguish the three conditions.

It contains all three conditions that is to be proven to the verifier, i.e.

• equality constraint involving $a(x),b(x),c(x)$
• permutation constraint:
  • $z(x)f^{\prime }(x)=g^{\prime }(x)z(x\omega )$
  • $L_1(z(x)-1)=0\forall x\in \text{Upomega}$

Round 4:

Evaluation of $a,b,c,S_{\sigma 1},S_{\sigma 2},t$ at $\mathfrak{z}$ and evaluation challenge: $z$ at $\mathfrak{z}\omega$. Namely, $\bar{a},\bar{b},\bar{c},{\bar{s}}_{\sigma 1},{\bar{s}}_{\sigma 2},\bar{z}$.

Round 5:

Linearisation polynomial $r(x)$ can be interpreted as $t(x)=t_{low}(X)+X^n{t}_{mid}(X)+X^{2n}{t}_{hi}(X)=l(X)/Z_H(X)$. Thus, prover proves $r(x)=l(X)-Z_H(\mathfrak{z})(t_{low}(X)+{\mathfrak{z}}^n{t}_{mid}(X)+{\mathfrak{z}}^{2n}{t}_{hi}(X))=0$, evaluated at $\mathfrak{z}$.

Proof polynomial: $W_{\mathfrak{z}}(x)=\frac{M(X)}{X-\mathfrak{z}}$, and $W_{\mathfrak{z}\omega }(x)=\frac{N(X)}{X-\mathfrak{z}\omega }$. It contains separate terms for each polynomial, separated using opening challenge: $v^i$. Send $[W_{\mathfrak{z}}{]}_1$ and $[W_{\mathfrak{z}\omega }{]}_1$.

Overall Proof:

Proof consists of:

1. 9 $G_1$ points: $[a{]}_1,[b{]}_1,[c{]}_1,[t_{low}{]}_1,[t_{mid}{]}_1,[t_{hi}{]}_1,[z{]}_1,[W_{\mathfrak{z}}{]}_1,[W_{\mathfrak{z}\omega }{]}_1$
2. 6 $\mathbb{F}$ evaluations: $\bar{a},\bar{b},\bar{c},{\bar{s}}_{\sigma 1},{\bar{s}}_{\sigma 2},\bar{z}$
3. multipoint evaluation challenge: $u$
4. $54(n+a)\log (n+a)\mathbb{F}mul$ operations

Verifier Algorithm

Explained intuition behind the steps really well here. Just reiterating those here:

$W_{\mathfrak{z}}(X)$ can be written as $M(X)/(X-\mathfrak{z})$, and $W_{\mathfrak{z}\omega }(x)=N(x)/(X-\mathfrak{z}\omega )$. Combining these two identities with multipoint evaluation challenge $u$, we get:

$$X(W(X)+u{W}_{\mathfrak{z}\omega }(X))=\mathfrak{z}W(X)+\mathfrak{z}\omega u{W}_{\mathfrak{z}\omega }(X)+M(X)+uN(X)$$

Plonk Extensions

• Turboplonk: Custom gates
• Ultraplonk: Turboplonk+ Plookup
• Hyperplonk
• UniPlonk
• Fflonk
• Goblinplonk

TurboPlonk

Plonk’s arithmetization allows to efficiently add gates other than addition/multiplication. These gates are necessary to reduce constraints in a repetitive computation like hash function computation which involves bitwise arithmetic like XOR.

This article from Kobi explains really well, the design considerations for a custom gate model of MiMc hash.

Plonkup

Explanation of prover and verifier’s algorithm with reasoning of each step can be found in a beautiful explanation in a blog post by Joshua and by Hector.

References

• ZK Whiteboard sessions
• Why and How ZK-SNARKS work?
• PLONK whitepaper
• Awesome PLONK
• ZKP MOOC L5
• Vitalik’s Understanding PLONK
• David Wong’s Understand PLONK
• Plonk by hand
• Plonk toy implementation
• ZK Proving systems by Jonathan Wang
• Plonk Arithmetization
• Gnark’s Plonk
• Zac: Adding zk to PLONK
• The Pantheon of Zero Knowledge Proof Development Frameworks
• zkHarness
• zkalc
• Jump: A primer on proof systems