Before understanding what even a dag based protocol does. First, we need to understand how it’s different than a traditional blockchain protocol like Bitcoin. A blockchain is a distributed ledger technology that can record and store data in a public, immutable, distributed chain. Participants can send transactions to the protocol that is recorded and confirmed as valid by global network nodes.

In a standard blockchain, only one single sequence of blocks is considered as canonical chain. Forks occurring in the protocol is identified as security threat as basically if a fork becomes too large, then it gives the malicious party more power in the network and affects the main chain of blocks. Validators/miners keep doing their work by batching the transactions in a block using a consensus rule and creating a block with it, which is then relayed to the entire network.

DAG protocols comes with a new idea, i.e. why not make every fork count. Why can’t a block have multiple parents? It is just a directed acyclic graph where a transaction added to the graph can have multiple parents and multiple children.

The idea of DAG-based BFT consensus (e.g., HashGraph and Aleph) is to separate the network communication layer from the consensus logic.

Terminology

Parties: A party $p$ is the one producing the blocks.
Nodes: A block is represented as a node in the DAG.
Edges: An edge is when a block $u$ points directly to another block $v$ . We say, $u$ acknowledges $v$ .
Observe: Transitive closure of acknowledge. Block $u$ observes $v$ , if there is a directed path from $u$ to $v$ .

Simple Payment Channel

N permissioned (blocks can include own set of transactions) parties produce blocks and points to all existing leaves.
works in asynchronous settings, i.e. Messages take finite amount of time to arrive.
Block $u$ approves $v$ produced by $p$ , if it observes $v$ and doesn’t observe any $p$ -block that equivocates with $v$ .
$p^{'}$ approves $v$ if some $p^{'}$ block approves $v$ .
Honest party $p^{'}$ can’t approve two equivocating blocks produced by $p$ .
Block $v$ is approved by supermajority if it is approved by $n - f$ parties, if $n > 3 f$ , then safety is achieved as two equivocating blocks produced by $p can’t be approved by a supermajority (due to quorum intersection).
Liveness is trivial as honest parties will keep producing blocks

Cordial Miners

dag-1

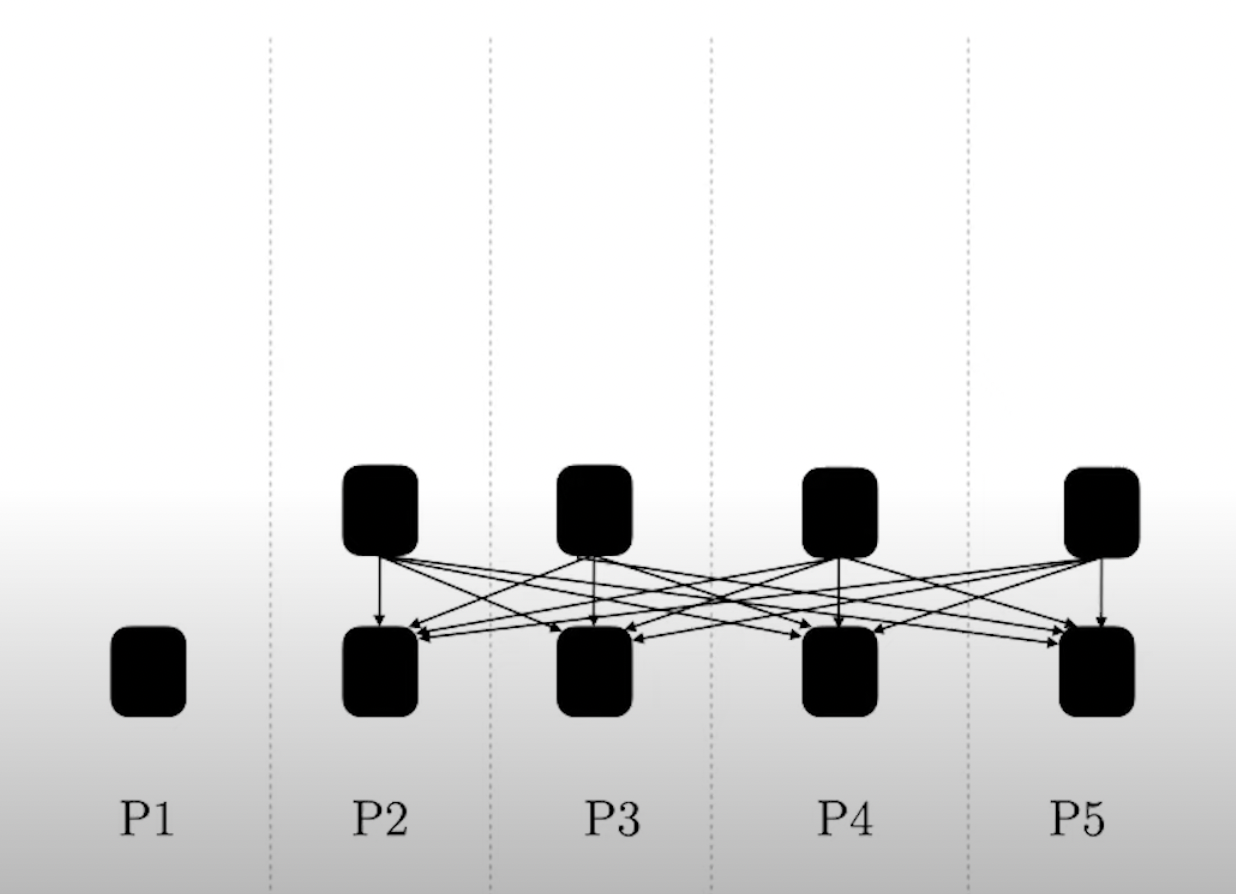
Give more structure to DAG.
have notion of rounds, with each honest party producing one block in each round.
an honest party produces block in round $r + 1$ , as soon as it sees $n - f$ blocks in round $r$ . The block produced in $r + 1$ must point to those $n - f$ blocks in round $r$ and also any leaves in previous rounds.
Have leader blocks, and $k$ consecutive rounds are called as wave (for cordial-miners $k = 5$ ). First round of each wave, select the leader. Block proposed by the leader at the first round will be called Leader Block.
Now, to get total ordering we need to extend the DAG, we suppose a function $τ$ which extends a partially ordered DAG to a totally ordered. Although only total ordering is not sufficient as we need to satisfy the SMR properties of safety and liveness.

Notation: For a block $u$ , $[u]$ denotes the initial segment of the DAG defined by $u$ .

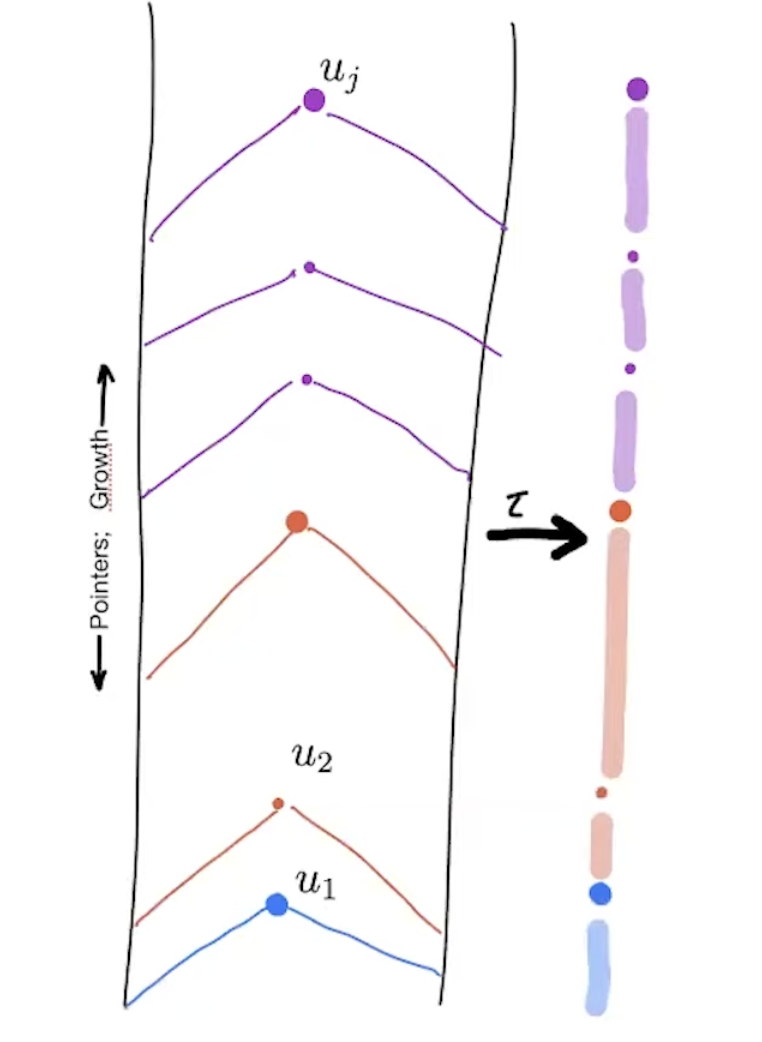
total-ordering

Now, the idea is to use $τ$ to arrange the leader blocks in some way such that total ordering is achieved. We define total ordering to be:

$τ ([u_{1}]) * τ ([u_{2} - u_{1}]) * \dots$

But we can’t use any leader blocks, there has to some concept of finality so that only final blocks are included in the total ordering.

Defining Finality

Supermajority of blocks means set of blocks produced by a supermajority of miners. A block $v$ is ratified by block $u$ if $[u]$ includes a supermajority of blocks approving $v$ . Can be thought of as seeing stage-1 QC for $v$ , thus producing stage-2 vote in tendermint sense.

Now a leader block of wave $w$ is final if it is ratified by a supermajority of blocks in the final round of wave $w$ . This is like $v$ receiving stage-2 QC vote in tendermint.

Now, define total ordering as: If dag $D$ has no final leader, then $or d (D) := ϕ$ else, let $u$ be the last final leader, then $or d (D) := τ^{'} (u)$ , where $τ$ is defined recursively:

$τ^{'} (u) := τ ([u]) or τ^{'} ([u^{'}]) * τ ([u] - [u^{'}])$

Since, we’ve defined our total ordering. All left now is to extract safety and liveness from total ordering.

Proving Safety

$L e mma .$ If a leader block is final, then it is ratified by every subsequent leader block.

$Cl aim .$ If $D_{1}$ , $D_{2}$ are DAGs held by honest parties $p_{1}$ , $p_{2}$ , then $or d (D_{1})$ and $or d (D_{2})$ are consistent.

Let’s assume the case where $D_{1} \subset D_{1} \cup D_{2}$ and $D_{2} \subset D_{1} \cup D_{2}$ , then $or d (D_{1})$ and $or d (D_{2})$ must be consistent with $or d (D_{1} \cup D_{2})$ . Let’s suffice to deal with the case $D_{1} \subset D_{2}$ .

Now, if $D_{1}$ has no final leader block, then as per definition of $or d$ , $or d (D_{1)} = ϕ$ . If $u$ is the final leader block then $u$ must be ratified by any subsequent leader block in $D_{2}$ .

Proving Liveness

$L e mma .$ Existence of inifinitely many honest final leader blocks.

Instead of announcing leader at the start of the round as then the leader can be delayed by the adversary, we let the parties produce the blocks and form DAG, then in the last round leader is selected randomly. This makes a scenario where all of the blocks in the last round ratify supermajority of the blocks from the first round and thus selecting a leader randomly now gives $> 2/3$ chance of selecting a final leader block for the wave.

DAG-Rider

Reliable Broadcast

Same as Byzantine broadcast but due to asynchronous setting, relax the termination condition.

Designate a broadcaster which has input $v \in V$
Agreement: If an honest party terminates, then all must terminate with the same output in $V$ .
Validity: If broadcaster is honest, then all honest parties must terminate giving the broadcaster’s input as their output.

Bracha’s Broadcast

Simple way to model reliable broadcast. Works in asynchronous setting.

broadcaster start with input $v$ , sends value to all
Three circumstances in which any party $p$ will speak:
- $p$ receives a first value $v$ from the broadcaster, they send $(ec h o, v)$ to all parties.
- $p$ receives $n - f (ec h o, v)$ messages from the parties and if $p$ hasn’t voted, then $p$ votes for $v$ by sending $(v o t e, v)$ to all parties.
- $p$ receives $(v o t e, v)$ from $f + 1$ distinct parties and $p$ hasn’t voted, then $p$ votes by sending $(v o t e, v)$ to all parties.

Similar to cordial miners but do not let equivocating blocks get added to the DAG. This is done using Reliable broadcast.

reduces number of round in each wave by 1.
But cost is to reliably broadcast the block which increases latency.
efficient version of reliable broadcast reduces amortized time complexity per transaction $O (n)$ for DAG-Rider.

Narwhal&Tusk

Decouples data dissemination from metadata ordering. Narwhal&Tusk paper introduced a highly scalable and efficient DAG construction method using Narwhal and total ordering of DAG with BFT properties using Tusk/Bullshark.

Narwhal

Narwhal off-loads reliable transaction dissemination to the mempool protocol.

Narwhal main task is to create a DAG using $N$ nodes in the network with upto $f < N /3$ byzantine nodes. Since, communication happens in an asynchronous network, Narwhal alone is not sufficient to guarantee liveness property and thus, Tusk/Bullshark was introduced that totally orders the DAG and satisfies BFT properties. DAG formation happens in a round-based structure.

Design Goals for Narwhal:

Reduce need for double transmissions when leaders propose blocks
enabling scaling out when more resources are available

Block Structure in Narwhal:

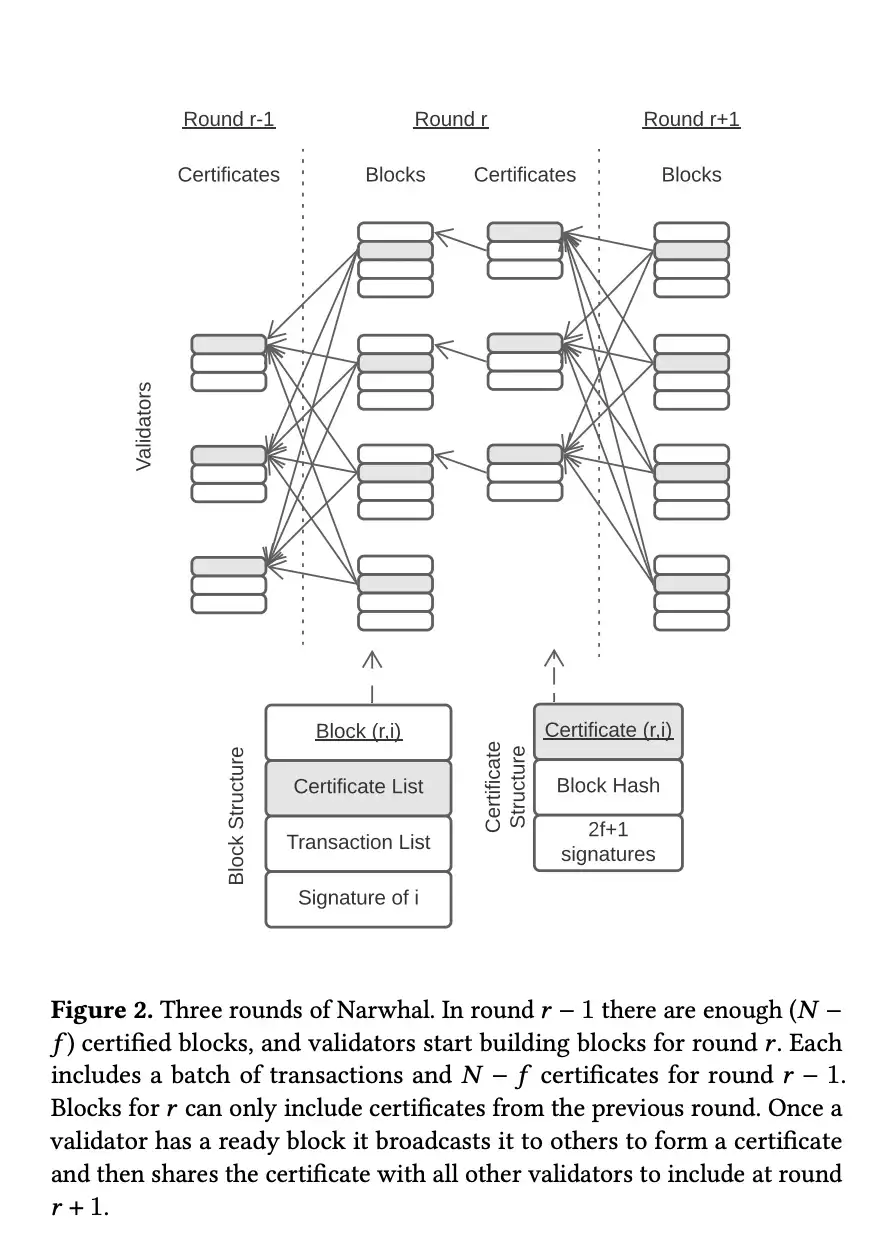
block_structure

A block $b$ consists of:

Set of transactions
$n - f$ block certificates from previous rounds
signature of $i$

The certificates encode a causal ‘happened-before’ relation between the blocks denoted as $b \to b^{'}$

Validators

Each validator consists of set of workers and a primary.
workers collect transactions from the clients and broadcast batches of data to workers.
Upon receiving $2 f + 1$ acks, workers forwards a digest of batches to primary.
primaries form a round-based DAG on metadata (vertices contain digests).
Thus, data dissemination is done by the workers at network speed regarding the metadata DAG construction by primaries.

Validators use following reliable broadcast protocol:

each validator sends metadata (digest of batches and $n - f$ references to previous rounds’ blocks) to all other validators.
each receiver replies with a signature if:
- workers sign a PoA so that the data corresponding to the digests is made available
- it has not replied to this validator in the round before (for non-equivocation)
sender sends a quorum certificate after getting $n - f$ such signatures.
validator advances to next round if it has received $n - f$ certificates from previous round.

Quorum Certificates has following advantages:

Non-equivocation: honest validators only sign one vertex per validator per round, and $n - f$ signatures are required to create a QC. Thus, byzantine validator won’t be able to create two different QC for different blocks due to quorum intersection.
Data availability: validators sign only if they locally store the data corresponding to the digests in the vertex.
history availability: a certificate of a block guarantees data availability, and certified blocks contain certificates from previous rounds. Thus, a validator store entire causal history of the block. A new validator joining can just learn about the DAG using certificates from previous rounds.

Thus, Narwhal satisfies following properties:

Integrity: For any digest $d$ , two different invocations of $re a d (d)$ to honest parties will return the same value.

This happens because honest parties can only reply with a signature when they’ve received the data corresponding to the digest.
Block-availability: If a $re a d (d)$ is invoked by an honest party after $w r i t e (d, b)$ succeeds for an honest party, then $re a d (d)$ eventually completes and returns $b$ .

$w r i t e (d, b)$ succeeds when sender has received $n - f$ certificates from other validators which signifies that they’ve received the data and will persist it. Thus, if a leader proposes a certificate, this means that the block will be available for later purposes.
2/3-Causality: successful $re a d_c a u s a l (d)$ returns a set $B$ that contains at least $2/3$ of the blocks written successfully before $w r i t e (d, b)$ succeeded.

To successfully write a block, a sender requires at least $n - f$ certificates from previous round signifying that the current proposed block references those causally ‘happened-before’ blocks. Thus, at least 2/3 of the blocks are included in the set.
1/2-Chain quality: At least half of the blocks in set $B$ returned by $re a d_c a u s a l (d)$ are written by honest parties.

Out of the $n - f$ certificates from previous round, at least half has to be honest due to assumption that $f < n /3$ .
Containment: let $B$ be the set returned by $re a d_c a u s a l (d)$ , then for every $b^{'} \in B$ , the set $B^{'}$ returned by $re a d_c a u s a l (d^{'})$ , $B^{'} \subseteq B$ .

Using Narwhal for Consensus

Narwhal as a high-throughput mempool can be combined with an asynchronous or eventually-synchronous protocol to achieve total-ordering. This is advantageous in many sense:

Same causal history of a block given a certificate. Any deterministic rule then can be used for total ordering
Bulk transaction information is evenly shared among all validators and doesn’t lead to uneven utilisation of resources
continues to work even in asynchronous environments, i.e. validators keep sending blocks and certificates.

Tusk

Like all protocols, Narwhal is also prone to impossibility result in asynchrony and thus, to retain liveness during asynchronous phase, Tusk was proposed in the Narwhal&Tusk paper which converts the causally ordered DAG to a totally ordered with zero extra communication.

Has a concept of waves which comprises of 3 rounds. Propose, vote, and produce randomness to elect a leader

lonerapier.xyz

Explorer

DAG-based consensus